티스토리 뷰
P5 - 안대 낀 스피드러너
https://www.acmicpc.net/problem/14451
14451번: 안대 낀 스피드러너
"전진, 우회전, 전진, 전진, 좌회전, 전진, 좌회전, 전진, 전진"의 순서를 따르면 6초 또는 9초만에 도착할 수 있다.
www.acmicpc.net
문제: N*N 격자에 각 칸은 비어 있거나 장애물이 있다. 왼쪽 아래 칸에서 시작해서 오른쪽 위까지 가야 하는데, 시작할 때 보고 있는 방향은 모른다. "전진", "좌회전", "우회전”을 최소 횟수만큼 사용해서 항상 목적지에 도달하는 방법을 찾아라.
풀이:
처음에 시작 가능한 상태가 두 가지 있고, 어떤 입력 순서가 주어졌을 때 1번 시작상태와 2번 시작상태가 위치한 곳은 확정적으로 구할 수 있다. 즉, 상태를 (1번 시작상태의 현재 위치) * (2번 시작상태의 현재 위치) * (두 상태의 회전 방향)과 같이 정하면, 대략 dp[20][20][20][20][4] 정도의 테이블에 모든 가능한 상태를 나열할 수 있다. (두 상태의 회전 방향 중 하나만 저장하면 나머지 하나도 구할 수 있어서, 방향 차원은 하나만 있으면 된다.)
각 상태는 최대 3개의 서로 다른 상태로 움직일 수 있다.(좌회전 / 우회전 / 직진) 따라서 이 상태들을 BFS로 순회하면서, dp[0][0][0][0][0]에서 dp[N-1][N-1][N-1][N-1][0..3] 으로 가는 최단거리를 구하면 된다.
P4 - 식사 계획 세우기
https://www.acmicpc.net/problem/25406
25406번: 식사 계획 세우기
사전 순의 정의 길이가 $N$인 순열 $X_1, X_2, \dots , X_N$이 길이가 $N$인 순열 $Y_1, Y_2, \dots , Y_N$보다 사전 순으로 앞선다는 것은 아래 조건과 동치이다. $X_i ≠ Y_i$가 성립하는 가장 작은 $i$ ($1 ≤ i ≤
www.acmicpc.net
문제: 길이 N의 배열 A가 주어진다. 길이 N의 순열 P를 만들었을 때, 모든 i에 대해 A[P[i]] != A[P[i+1]] 조건을 만족하면 올바른 순열이다. 올바른 순열 중 사전순으로 가장 앞선 것을 찾아라.
풀이:
그리디하게 사전순으로 가장 작은 순열을 만들면 된다. 자명하게 불가능한 케이스를 처음에 빼면, 그리디하게 순열에 원소를 하나씩 추가하는 과정 중에 아래와 같은 두 가지 케이스가 있을 것이다.
- 어떤 한 음식의 종류가 남은 음식의 과반을 차지할 경우, 반드시 그 음식 종류를 사용해야 한다. 그 음식 종류를 가진 음식 중에서 가장 인덱스가 작은 것을 쓰면 된다.
- 그 외의 경우에는, 바로 전에 쓴 음식의 종류와 겹치지 않는 음식 중 가장 인덱스가 작은 것을 쓰면 된다.
이 두 가지 케이스에서 어떤 인덱스를 사용할 것인지 빠르게 판별할 수 있기만 하면 되는데, 여기서부터는 다양한 자료구조를 사용하는 여러 가지 방법이 있을 것 같다. 나는
- "특정 음식 종류가 과반을 넘겼는지" 판단하기 위해서 set에 {음식 종류 내 남은 음식 개수, 음식 종류} pair를 유지했고 (priority_queue같은 걸로도 될 것)
- 특정 음식 종류의 음식 중에서 가장 인덱스가 작은 것을 가져오기 위해서 각 음식 종류에 있는 음식을 vector<vector<int>> 로 관리하고
- 바로 전에 쓴 음식의 종류와 겹치지 않는 음식 중 가장 인덱스가 작은 것을 구하기 위해서 이미 먹은 음식을 체크하는 bool 배열을 유지하면서, 이 위에서 포인터 두 개로 가장 인덱스 작은 것 + 그게 겹쳐서 안되면 대신 쓸 것을 유지했다. (아마 set을 잘 쓰면 좀 더 수월할수도..)
코드: https://www.acmicpc.net/source/share/19bbb66668a94a1493b3668526aece77
P3 - 차이를 최소로
https://www.acmicpc.net/problem/3090
3090번: 차이를 최소로
각각의 테스트 케이스에 대해서, 점수는 (100×(S+1)/(D+1))/(데이터 개수) 점이다. 이때, D는 출력한 수열에서 인접한 수의 차이의 최댓값, S는 정답이다. 즉, 출력한 수열이 정답인 경우 10점을 얻게
www.acmicpc.net
문제: 길이 N의 배열 A가 있고, 수열의 수 하나를 골라서 값을 1 감소시킬 수 있다. 단, 수는 1보다 작아질 수 없다. 감소 연산을 최대 T번 할 때, 인접한 수의 차이의 최댓값을 최소로 해야 한다.
풀이:
"인접한 수의 차이의 최대값을 X로 하는 것이 가능한가" 라는 결정문제를 NlogN 정도에 풀 수 있으면, 이분탐색으로 전체 문제를 풀 수 있다.
해당 결정문제를 푸는 방법은 두 가지가 있는 것 같다.
- 가장 낮은 숫자는 더 이상 낮출 필요가 없을 테니까, 가장 낮은 숫자부터 시작해서 주변의 숫자와의 차이가 X보다 크다면 주변의 숫자를 낮춘다. priority queue를 사용해서 현재 남아있는 숫자중에 가장 낮은 숫자를 찾을 수 있다. 다익스트라랑 비슷하다. 코드: http://boj.kr/f5670d5e38984f61859410f3fddd77a3
- 숫자를 왼쪽에서부터 보면서 각 숫자의 왼쪽 숫자와의 차이가 X보다 크다면 왼쪽 숫자를 낮추고, 다시 숫자를 오른쪽에서부터 보면서 각 숫자의 오른쪽 숫자와의 차이가 X보다 크다면 오른쪽 숫자를 낮춘다. 다른 블로그들을 보면 다 이 풀이를 사용하고 구현도 더 쉬운데, 직관적으로 떠올리기 쉽지 않은 것 같다. 곰곰히 생각해보면 첫 번째 방법이 커버하는 케이스를 다 커버하긴 하는 것 같다.
P2 - 크래이피쉬 글쓰는 기계
https://www.acmicpc.net/problem/5812
5812번: 크래이피쉬 글쓰는 기계
활자 인쇄기를 발명한 독일 대장장이인 요하네스 구텐베르크는 레오나르도가 열렬히 존경하는 사람이었다. 레오나르도는 크래이피쉬 글쓰는 기계 — il gambero scrivano —로 불리는 매우 단순한
www.acmicpc.net
문제: 빈 문자열에서 시작해서 문자 L 추가, 최근 U개의 명령어 취소 두 가지 명령으로 문자열을 변경할 수 있다. 중간중간에 P번째 문자를 질의하는 쿼리에 응답해야 한다.
풀이:
Undo를 하더라도 기존의 상태를 유지하는 Persistent Data Structure를 관리할 수 있다.
구체적으로, 문자열을 linked list와 같이 node간의 연결로 표시해 두고, 각 연산이 완료된 시점에 가르킬 node index를 저장해 둔다. T연산에서는 노드를 하나 추가하고, 연산 완료 시점에는 새로 추가한 node를 가르킨다. U연산은 u개의 연산을 뒤돌아간 시점에 가르키고 있는 node를 같이 가르키면 된다.
아래 그림에서 조금 더 자세히 볼 수 있다.
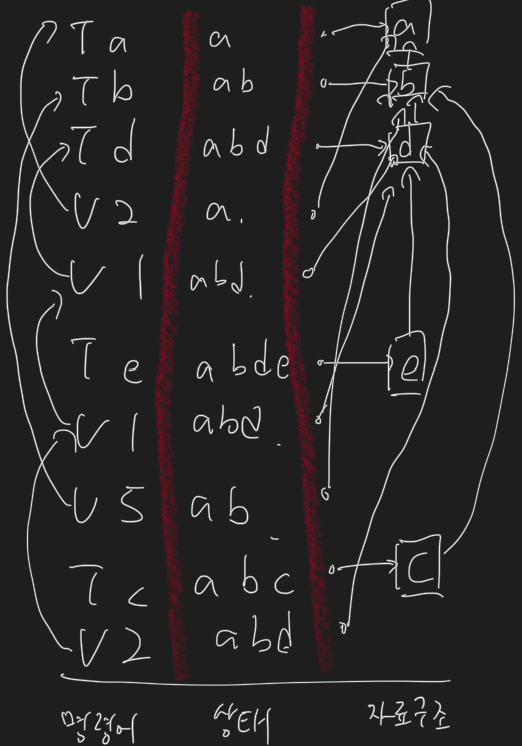
P연산을 해결하기 위해서는 노드 N개를 log(N)시간에 건너뛰어야 하는데, 이건 sparse table로 연산당 log(N)에 해결할 수 있다. (https://cp-algorithms.com/data_structures/sparse-table.html#range-sum-queries) 물론 이러면 T연산도 log(N)이 된다.
P1 - 코끼리
https://www.acmicpc.net/problem/3133
3133번: 코끼리
N개의 식물이 표면에 떠 있는 호수에 코끼리 한 마리가 살고 있다. 이 호수는 각각의 식물들이 정수 좌표에 있는 좌표평면으로 나타낼 수 있다. 매일 아침마다 이 코끼리는 식물들 위를 신나게
www.acmicpc.net
문제: 좌표평면 위에 식물이 N개 주어진다. 코끼리는 임의의 식물에서 시작해서 x와 y좌표가 모두 더 큰 점으로 뛸 수 있다. 최대로 뛸 수 있는 식물의 개수를 계산하고, 그렇게 뛸 수 있는 방법의 수를 계산하자.
풀이:
i 식물에서 끝나는 최장 경로의 길이와, 그렇게 할 수 있는 경우의 수를 dp_i, cnt_i로 표현해보자. i번 식물보다 x와 y가 모두 더 작은 식물들 중, 가장 큰 dp값이 dp_i가 되고, 또 그 dp값을 가진 식물들의 cnt를 모두 합친 것이 cnt_i가 된다.
이제 각 식물마다 x와 y가 모두 더 작은 식물들에 대해서 위 방법으로 dp_i, cnt_i를 순차적으로 구하면 된다. 점들을 정렬해서 순회하면 각 점을 순회할 때 x와 y가 모두 더 작은 식물들을 이미 순회했음을 보장할 수 있다.
이제 각 식물에 대해서 가장 큰 dp값과 그 dp값을 가진 식물들의 cnt의 합을 빠르게 구해야 하는데, 이건 세그먼트 트리를 쓸 수 있다. 조금 더 자세히 설명하자면, 세그먼트 트리의 각 노드에는 {dp, cnt}값을 저장하고, 점들을 y좌표가 증가하는 순서대로 보면서 (x, y)좌표에 있는 식물에서는 세그먼트 트리의 [0, x)번 리프 노드의 합을 조회하고, 그렇게 구한 dp, cnt값을 다시 x번 리프노드에 point update해준다고 생각하면 된다.
이 문제는 점이 정렬된 순서로 들어온다고 보면 2차원 상의 LIS와 비슷하게 볼 수 있는데, 1차원 LIS의 길이와 개수를 세는 문제인 https://www.acmicpc.net/problem/17411 를 풀어보면 도움이 될 것 같다.
- Total
- Today
- Yesterday
- Counting
- segtree
- induction
- subsequence
- fenwick
- GREEDY
- subarray
- offline
- merge sort tree
- 규칙찾기
- 문자열 알고리즘
- sqrt decomposition
- dp
- offline query
- 기하
- range query
- tree
- bitmask
- 비둘기집의 원리
- 트라이
- line sweeping
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
