티스토리 뷰

BOJ 1559 - 놀라운 미로 (P5)
https://www.acmicpc.net/problem/1559
1559번: 놀라운 미로
입력 데이터는 여러 개의 테스트 케이스로 구성되어 있다. 각각의 입력은 두 정수 M, N(2 ≤ M, N ≤ 100)으로 시작하며, 다음 M개의 줄에는 초기에 문이 열린 방향을 나타내는 N, E, S, W중 하나의 문자
www.acmicpc.net
문제: M*N미로에서, 각 칸마다 한 방향으로 문이 열려있고 이 방향은 매 초 시계방향으로 회전한다. 1,1에서 시작해서 M,N까지 가면서 모든 보물상자를 모아야 한다.
풀이:
먼저, 보물상자의 개수가 최대 8개임으로 각 보물상자를 먹었는지 여부를 256 미만의 비트마스크로 표현할 수 있다. 따라서 "dist[r][c][bm] = (r, c) 위치에 있고 보물상자 먹은 상태가 bm 비트마스크에 대응될 때, 해당 상태까지 가기 위한 최단 거리" 로 정의할 수 있다.
일반적인 그리드 문제라면 여기서 bfs로 풀 수 있겠지만, 이 문제가 조금 다른 점은 제자리에 그대로 있어야 할 때도 있다는 점이다. 따라서 이 상태정의 그대로 bfs를 돌리기는 어렵다. 이 문제를 푸는 방법 중 하나는, 각 위치에서 네 방향으로 각각 길이 1,2,3,4의 간선이 하나씩 있다고 간주하고 다익스트라를 돌리는 것이다. 즉 현재 방향이 E 라면, E방향으로는 길이 1, S 방향으로는 길이 2.. 이런 식으로 4개의 간선이 있다고 생각하는 것이다. 이렇게 다익스트라를 돌리고 나면 답은 dist[R][C][(1<<K-1] 이 된다.
코드: https://www.acmicpc.net/source/share/52bb744526514d7da0bb4d8eec37401f
BOJ 9623 - 부분 수열의 길이 (P4)
https://www.acmicpc.net/problem/9623
9623번: 부분 수열의 길이
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 N (1 ≤ N ≤ 500,000)과 X (-109 ≤ X ≤ 109)가 주어진다. 둘째 줄에는 수열에 들어있는 정수 N개가 주어진다. 이 정수는
www.acmicpc.net
문제: 길이가 N인 정수 수열과 정수 X가 주어진다. 이때, 합이 X보다 크거나 같은 연속 부분 수열 중에서 길이가 가장 짧은 것을 찾는 프로그램을 작성하시오.
풀이:
각 인덱스별로, 해당 인덱스에서 끝나면서 합이 X보다 크거나 같은 연속 부분 수열 중에서 길이가 가장 짧은 것을 찾는 것을 목표로 하자. 이를 위해서는, (주어진 배열을 A, 그리고 A의 부분합 배열을 S라고 한다면) i번 위치에서 j < i인 j에 대해서 S[j] <= S[i] - X인 j 중에서 가장 큰 j를 골라야 한다.
후보가 될 수 있는 j는 S[j]가 작을수록 더 유리하고, 주어진 기준 이하로 작다면 j 자체가 클수록 유리하다. 즉 후보가 될 수 있는 두 j인 j1, j2에 대해서 S[j1] < S[j2] 이고 j1 > j2라면 j1은 j2의 상위호환이 된다. 즉, monotonic queue랑 비슷하게 상위호환이 존재하는 j는 제거된 상태에서 j값과 S[j] 모두 단조증가하는 배열을 만들 수 있고, 이 배열에서 원하는 S[j] 보다 작은 마지막 위치에 원하는 j를 이분탐색으로 찾을 수 있다.
i번 인덱스를 이 배열에 추가할 때는 배열의 단조성을 유지해야 하고, 배열의 맨 마지막 원소가 S[i] 보다 큰 합을 가지고 있다면 반복적으로 마지막 원소를 제거해주는 작업을 수행한 뒤에 {i, S[i]}를 해당 배열에 추가하면 단조성이 유지된다.
코드: https://www.acmicpc.net/source/share/03e07058a1134a66b1023a3444de2887

BOJ 2679 - 맨처스터의 도로 (P3)
https://www.acmicpc.net/problem/2679
문제: 단방향 그래프로 표현되는 도로에서, 각 간선에 1시간에 지나갈 수 있는 차의 개수 제한이 있다. 이 그래프에서 모든 도로를 사용했을 때 1시간 동안 A에서 B에 도착할 수 있는 차의 최대 개수와, 그래프에서 경로 딱 하나만 사용했을 때 1시간 동안 A에서 B에 도착할 수 있는 차의 최대 개수의 비율을 구하자.
풀이:
먼저, 모든 도로를 사용했을 때 1시간 동안 A에서 B에 도착할 수 있는 차의 최대 개수를 구하는 것은 단순한 유량 문제이다. A에서 B로 가는 최대 유량을 구하면 된다.
경로 딱 하나만 사용했을 때 1시간 동안 A에서 B에 도착할 수 있는 차의 최대 개수는, 다익스트라와 비슷하게 시작점에서부터 시작해서 각 노드별로 차가 최대 몇 대 도착할 수 있는지 확정짓는 방식을 쓸 수 있다.
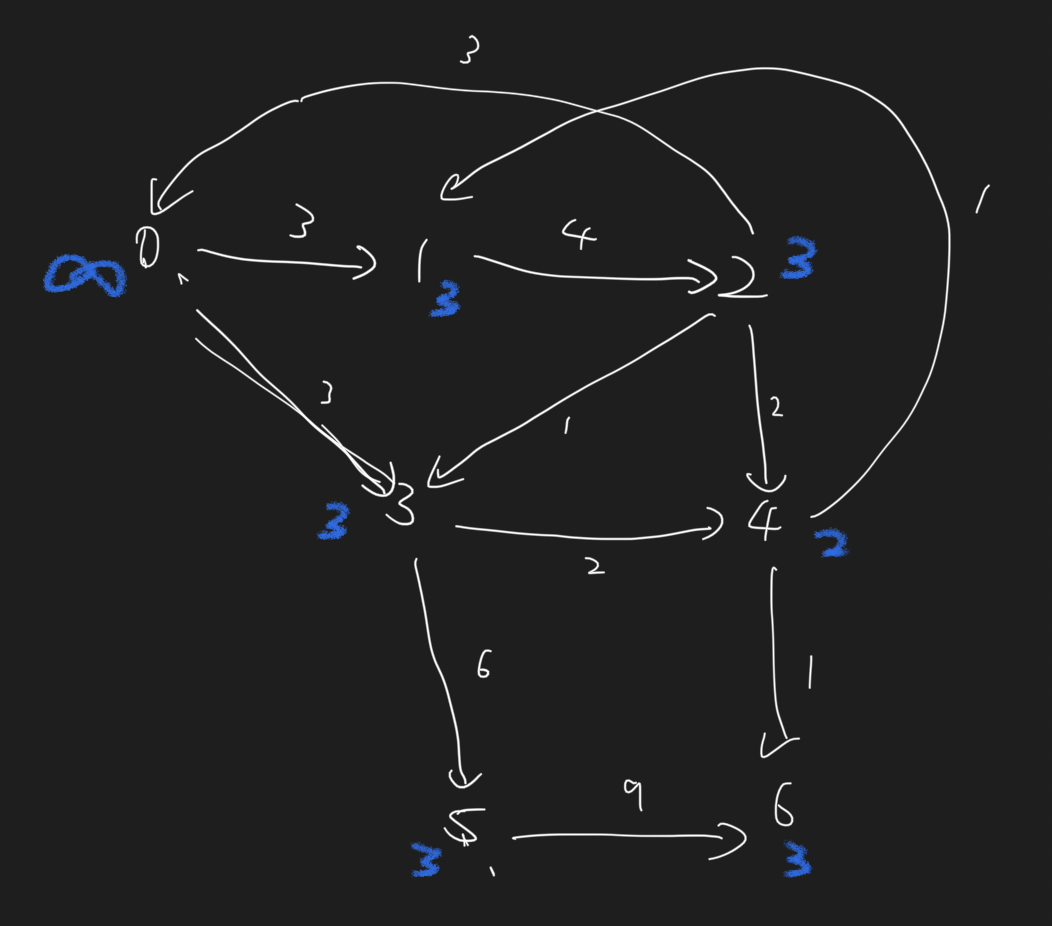
예를 들어서 예제에서는 0번 노드에서 시작하니, 0번 노드에 도착할 수 있는 차의 최대 개수는 무한대이고, 그 외 다른 노드에 도착할 수 있는 차의 최대 개수는 0에서부터 시작된다. 여기서 3번 노드로 갈 때는 길 제한이 3이니, 3번 노드에 도달하는 최대 차 개수는 3이 된다. 여기서 3번 노드에서 4번 노드로 갈 때는, 4번 노드의 최대 차 개수는 2가 된다. 다익스트라와 비슷하지만 여기서는 일반적인 다익스트라와 반대로 차 개수가 많으면 많을수록 좋은 거니까, 차 개수가 더 많아지게 할 수 있을 때 relax하는, 다익스트라와 반대되는 방향의 relax를 사용하면 된다.
코드: http://boj.kr/06da9d2bb0204e7eaceb88d99001d19f
BOJ 10413 - 반복되는 부분 문자열(P2)
https://www.acmicpc.net/problem/10413
10413번: 반복되는 부분 문자열
각 테스트 케이스마다, 주어지는 문자열에서 반복되는 모든 유일한 부분 문자열의 개수를 출력한다. 이때, 답은 부호있는 32비트 정수형으로 항상 표현할 수 있다.
www.acmicpc.net
문제: 주어진 문자열에서, 반복되는 부분 문자열의 개수를 찾자.
풀이:
먼저 suffix array와 LCP array을 만들자. 해당 개념은 https://cp-algorithms.com/string/suffix-array.html 여기서 더 자세히 확인할 수 있다.
LCP array를 통해서 인접한 suffix pair n-1개 각각에 대해 반복되는 부분 문자열의 개수를 알 수 있다. 예를 들어서, "aabaab" 에 대해 suffix array를 만들면 가장 앞에 있는 두 suffix는 "aab"와 "aabaab"가 되는데, 이 suffix pair는 lcp값이 3이고, 이에 대응되는 반복되는 부분 문자열 3개가 존재한다. (a / aa / aab)
suffix pair n-1개 각각이 만드는 반복되는 부분 문자열의 개수(즉, lcp array의 모든 수)를 단순히 더하면 중복이 발생한다. 이를 방지하기 위해서는, 먼저 lcp array의 합을 구하고, 거기서 인접한 lcp array의 원소 pair마다 두 값 중 작은 것을 합에서 빼주면 중복된 부분 문자열을 모두 제거할 수 있다. lcp array상 인접한 두 수의 경우, 더 작은 수에 대응되는 부분 문자열들이 더 큰 수에 대응되는 부분 문자열들에 완전히 포함되기 때문이다.
코드: http://boj.kr/f85fee4e0fdf49b78fc170100d5d1042

BOJ 5009 - 유치원 (P1)
문제: N명의 학생들을 세 개의 반에 배정시키는데, 기존과 같은 반에 배정되면 안된다. 각 학생은 다른 학생에 대한 선호도가 있는데, 이때 각 반에 있는 모든 학생들이 서로에 대한 선호도가 상위 T등 안에 들게 하는 가장 작은 T를 찾아야 한다.
풀이:
총 반 개수가 3개이기 때문에, 각 학생마다 가능한 반이 두 개 있다. 따라서 "i번 학생이 가능한 첫번째 반에 속함", "i번 학생이 가능한 두번째 반에 속함"과 같이 각 학생마다 두 개의 불리언 명제를 만들 수 있고, T를 고정하고 보면 해당 문제를 2N개의 불리언 명제를 제약사항을 위반하지 않고 값을 할당할 수 있는지 판단하는 것으로 환원해서 생각할 수 있다.
2-SAT에 맞게 제약사항을 표현할려면, 아래와 같이 할 수 있다.
- "i번 학생이 가능한 첫번째 반에 속함" / "i번 학생이 가능한 두번째 반에 속함" 두 명제 중 정확히 하나만 참이어야 한다. 이런 관계는 (A | B) & (~A | ~B) 와 같이 표현할 수 있다. 즉, 각 학생마다 OR문 두개를 만들자.
- i번 학생과 j번 학생의 선호도가 T등 밖에 있어서 두 학생이 같은 반에 있을 수 없다면, i번 학생과 j번 학생이 같은 방에 있는 것을 가르키는 두 명제가 동시에 참이 되지 않게 해야 한다. 이런 관계는 ~A | ~B 와 같이 표현할 수 있다. 즉, 같은 방에 있을 수 없는 학생 쌍 하나마다 OR문 하나를 만들자.
T를 고정했을 때에는 이렇게 2-SAT에 해당하는 식을 만들어서, 식이 참이면 해당 T도 가능한 것으로 판정할 수 있다. 가능한 T 중에 가장 작은 T는 이분탐색을 해도 되고, 순차적으로 찾아도 제한이 작아서 시간초과는 나지 않는다.
- Total
- Today
- Yesterday
- range query
- sqrt decomposition
- 규칙찾기
- line sweeping
- subsequence
- merge sort tree
- 트라이
- Counting
- 기하
- subarray
- GREEDY
- 문자열 알고리즘
- dp
- offline query
- bitmask
- tree
- fenwick
- offline
- segtree
- 비둘기집의 원리
- induction
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
