티스토리 뷰

BOJ 1979 - 극적인 곱셈 (P5)
https://www.acmicpc.net/problem/1979
1979번: 극적인 곱셈
첫째 줄에 구한 n-극적인 숫자 중 마지막 숫자가 k인 수를 출력한다. 그런 숫자가 존재하지 않는 경우에는 0을 출력한다.
www.acmicpc.net
문제: n을 곱했을 때 오른쪽으로 숫자가 한 칸씩 옮겨진 수가 되는 수를 n-극적인 수라고 부른다. n-극적이면서 마지막 숫자가 k인 수를 찾는 문제다.
풀이:
우선, n = 1일 때는 답이 k이다. 이 부분을 먼저 처리한다.
k가 마지막 자리에 있는 n-극적인 숫자는, n을 곱한 후에는 k가 첫 번째 자리로 가고, 나머지 숫자들은 자리만 한 칸씩 이동한다. k를 제외하고 나머지 숫자들로 이루어진 수를 x라고 생각해보자. (ex. 예제의 128205같은 경우, x = 12820이고 k=5) 그러면 아래 그림처럼 식을 세워서, x가 i자리일때 x를 구하는 식을 정리할 수 있다.

정리하면 x = k(10^i - n) / (10n - 1) 과 같이 x를 구할 수 있고, 해당 값을 정수로 만들 수 있을 때까지 i를 늘려가면서 찾으면 된다. 대략 60자리까지 필요하기 때문에, 파이썬을 활용하면 편리하다.
BOJ 1637 - 날카로운 눈 (P4)
https://www.acmicpc.net/problem/1637
1637번: 날카로운 눈
첫째 줄에 입력의 개수 N이 주어진다. N은 1이상 20,000이하인 수이다. 그 다음 줄부터 N줄에 걸쳐 세 개의 정수 A, C, B가 주어지는데, 이것은 A, A+B, A+2B, ..., A+kB (단, A+kB ≦ C) 의 정수들이 정수더미
www.acmicpc.net
문제: 정수더미가 N개 주어진다. 각 정수 더미는 A+kB (0 <= k <= C) 로 표현되는 정수를 표현한다. 이 정수 더미들에 있는 수를 모두 모으면 홀수개 존재하는 정수가 최대 한 개 있는데, 이 정수를 찾는 문제이다.
풀이:
홀수 개 있는 유일한 정수를 x라고 하자. x를 포함하는 구간에 대해서 모든 정수의 개수를 센다면, 홀수개의 정수가 있을 것이다. (다른 정수는 모두 짝수개) 이 점을 이용해서, x를 찾기 위해서 이분탐색을 할 수 있다. 전체 구간의 앞 절반에 있는 정수 개수의 홀짝성을 확인하고, 개수가 짝수면 뒤 절반에서 계속 x를 찾고, 개수가 홀수면 앞 절반에서 x를 찾는 방식이다.
구간 내에 정수가 몇 개 있는지 세는 것은, 각 정수 더미마다 구간 내의 정수가 몇 개 있는지 O(1)에 계산할 수 있기 때문에, 전체 정수 더미를 모두 보면 O(N)에 셀 수 있다.
추가로, 구현상의 트릭이 하나 있다. [a, b] 구간 내의 정수 개수의 홀짝성을 판단할 때, 정직하게 [a, b]의 범위 내의 정수 개수를 셀 필요는 없고, [1, b]구간의 정수 개수만 세면 충분하다. (홀수 개수의 수가 정확히 하나 있으니까, [a, b]구간에 대해 이분탐색을 하고 있을 때 [1, a-1]구간의 개수는 어처피 짝수개이기 때문) 이렇게 하면 구현시 정수 더미에 대해 b를 넘어가는 수만 빼고 세면 되니까 구현이 조금 더 쉬워진다.
코드: https://www.acmicpc.net/source/share/cd98a493582049f8b5d946af32190197
BOJ 5000 - 빵 정렬 (P3)
https://www.acmicpc.net/problem/5000
5000번: 빵 정렬
첫째 줄에 빵의 개수 n (3 ≤ n ≤ 100,000)이 주어진다. 둘째 줄에는 빵의 현재 순서가 주어지고, 셋째 줄에는 사장이 원하는 빵의 순서가 주어진다. 빵은 1부터 n까지 숫자로 나타낼 수 있다. 두 빵
www.acmicpc.net
문제: 빵의 배열이 하나의 permutation으로 주어지고, 이 중에서 연속된 3개의 빵에 대해 가장 오른쪽 빵이 왼쪽으로 가고, 나머지 빵은 오른쪽으로 한 칸 이동하도록 할 수 있다. 이 연산으로 첫 번째 빵 배열을 두 번째 빵 배열로 만들 수 있는지 구하라.
풀이:
솔루션 자체는 간단하게 설명할 수 있다.
> 문제에서 주어진 연산은 inversion count의 홀짝성을 바꾸지 않는다.
> 따라서, iff 입력된 두 배열의 inversion count의 홀짝성이 같으면 possible이다.
내가 풀이에 접근했던 방식도 적어보자면.. 이 문제에서는 가장 작은 케이스에서 시작해서 규칙을 찾을려고 시도해본게 유용했다. 예를 들어서, 이 문제에서는 길이가 3인 permutation들에 대해서, 어디서 어디로 도달할 수 있는지 손으로 쉽게 그려볼 수 있다.

이렇게 작은 케이스를 그려보면, inversion count로 접근할 수 있다는 힌트를 상대적으로 쉽게 얻을 수 있다.
코드: https://www.acmicpc.net/source/share/7027681b79694c659980fedea4e96d30
공유 소스 보기
www.acmicpc.net
BOJ 9537 - 잘생긴 GCD (P2)
https://www.acmicpc.net/problem/9537
9537번: 잘생긴 GCD
입력은 여러개의 테스트 케이스로 이루어진다. 첫 줄에는 테스트 케이스의 수를 의미하는 T 가 주어진다. 각 각의 테스트 케이스들은 두 줄로 구성되는데, 첫 줄은 수열의 크기 n ( 1 ≤ n ≤ 100
www.acmicpc.net
문제: 어떤 수열의 잘생긴 GCD는, 그 수열의 모든 원소들의 최대공약수에 수열의 길이를 곱한 값으로 정의된다. 주어진 수열의 모든 subarray에서 가장 큰 잘생긴 GCD값을 찾는 문제.
풀이:
각 원소마다, 해당 원소에서 시작하는 가장 큰 잘생긴 GCD값을 찾아보자. 어떤 특정 원소에서 시작해서 뒤로 원소를 하나하나 추가하다 보면, GCD값이 더 작아지는 순간이 있고, 항상 해당 순간 전까지의 subarray를 사용하는 것이 그렇지 않은 것보다 더 낫다. 예시로, 아래 그림과 같은 배열에서, 210*4, 30*6, 6*9, 2*10 네 가지 경우만 고려하면 된다.
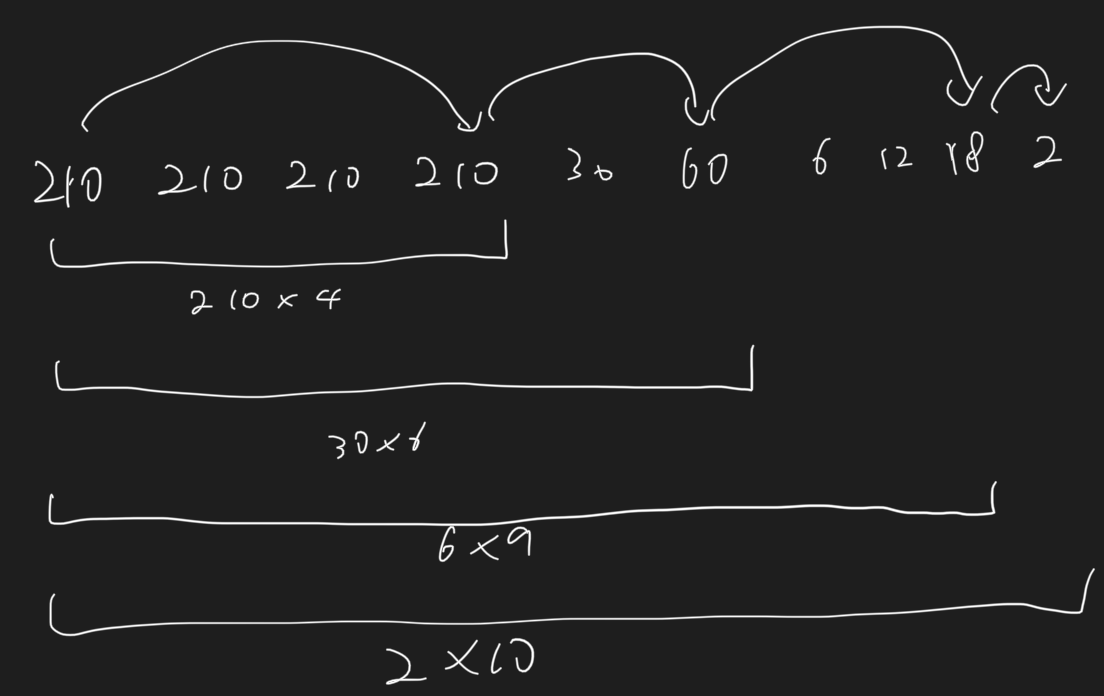
GCD값이 더 작아질 때 최소 2배는 작아지기 때문에, GCD값이 더 작아지는 순간은 최대 log2(10^12)번 존재한다. 각 위치에서 다음으로 현재 GCD값이 더 작아지는 순간은, 구간의 GCD를 저장하는 sparse table을 미리 전처리해두면, binary lifting하는 방법과 유사하게 log2(N)시간에 찾을 수 있다.
시간복잡도는 Nlog2(N)log2(10^12) 이다.
코드: https://www.acmicpc.net/source/share/92f231f435b64e8686a9e7d51a666360
공유 소스 보기
www.acmicpc.net
- Total
- Today
- Yesterday
- 트라이
- offline query
- offline
- merge sort tree
- fenwick
- 기하
- subsequence
- segtree
- subarray
- induction
- 비둘기집의 원리
- Counting
- dp
- bitmask
- tree
- line sweeping
- 문자열 알고리즘
- range query
- GREEDY
- 규칙찾기
- sqrt decomposition
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
