티스토리 뷰

BOJ 10792 - Ship Traffic
https://www.acmicpc.net/problem/10792
10792번: Ship Traffic
The first line of input contains six integers: the number of lanes n (1 ≤ n ≤ 105), the width w of each lane (1 ≤ w ≤ 1 000), the speed u of ships and the speed v of the ferry (1 ≤ u, v ≤ 100), the ferry’s earliest start time t1 and the ferry
www.acmicpc.net
문제: N행의 배가 일정한 속도로 지나가고, 내 페리선이 수직 방향으로 일정한 속도로 배들 사이를 지나가는데, 이 때 지나가면서 배와 부딪히지 않으면서 지나갈 수 있는 가장 긴 시간 구간을 구하는 문제다.
풀이:
문제 상황은 복잡하지만, 몇 가지 방식으로 더 간단하게 만들 수 있다.
- 배의 시작 / 끝 위치를, 페리가 지나는 수직 라인을 지나는 시간으로 변환
- 배의 시작 시간이 실제 수직 라인을 지날 때 보다 W / V초 이전부터 수직 라인을 지나가도록 변환 (페리가 한 lane을 지나가는 시간을 고려)
- i번째 레인에서는 i * (W / V)초 더 빨리 수직 레인에 도달하도록 변환 (모든 lane을 동일하게 취급할 수 있도록)
이렇게 하면 문제는 여러 개의 시간 간격이 있고, [T1, T2] 사이에서 이 시간 간격들이 점유하지 않는 가장 긴 비어있는 간격을 구하는 문제가 된다. 이 문제는 시작점과 끝점을 모아서 정렬해두고, 시작점일때 +1, 끝점일때 -1로 카운터를 설정해주고, 카운터가 0에 도달했을 때 해당하는 비어있는 구간의 길이를 구하는 방식으로 풀 수 있다.
코드: https://www.acmicpc.net/source/share/75ccdcfa479844d49fe38bd37bd9cd80
BOJ 10787 - Cutting Cheeze
https://www.acmicpc.net/problem/10787
10787번: Cutting Cheese
The first line of the input contains two integers n and s, where 0 ≤ n ≤ 10 000 is the number of holes in the cheese, and 1 ≤ s ≤ 100 is the number of slices to cut. The next n lines each contain four positive integers r, x, y, and z that describe
www.acmicpc.net
문제 요약: 정육면체의 치즈 내에 여러 개의 sphere 구멍이 나 있을 때, 이 치즈 덩어리를 z축에 수직으로 잘라 S등분하는 방법을 찾는 문제.
풀이:
이분탐색으로 잘라야 할 z좌표를 하나하나 찾으면 된다. 잘랐을 때 한 덩이의 부피는 (정육면체의 부피 - sphere 구멍들의 부피) / S이니까, z좌표상으로 왼쪽 끝과 오른쪽 끝을 정하고, 이 구간의 부피가 우리가 원하는 한 덩이의 부피보다 작으면 오른쪽 끝을 늘리고, 아니면 줄이는 식으로 잘라야 할 z좌표를 찾을 수 있다.
z좌표상으로 왼쪽 끝과 오른쪽 끝이 정해져 있을 때 해당 구간의 부피를 구하는 것은, 각 sphere에 대해서 구간 밖에 있는 Spherical cap의 부피를 계산해서 빼는 방식으로 구할 수 있다. https://en.wikipedia.org/wiki/Spherical_cap
코드: https://www.acmicpc.net/source/share/ea9e519e85a94cd68ceb3068a58fe3bd
BOJ 10789 - Keyboarding
https://www.acmicpc.net/problem/10789
10789번: 가상 키보드 입력
입력의 첫 번째 줄(행)에는 두 개의 정수 r과 c (1 ≤ r, c ≤ 50)가 포함되어 가상 키보드 격자의 행과 열 수를 제공합니다. 가상 키보드는 다음 r 행에 표시되며 각 행에는 c 문자가 들어 있습니다.
www.acmicpc.net
문제 요약: 가상 키보드가 주어지고, 여기서 상, 하, 좌, 우 네 개 방향으로만 움직여서 원하는 문자열을 타이핑해야 한다. 움직이는 횟수를 최소화하는 문제.
풀이:
"seen[r][c][h] = (r,c)위치에 있고, h번째 글자를 쳐야 하는 상태에 도달했는지 여부"로 정의하자. 이 상태정의에서 bfs를 돌려서, H = len(Text) 일때 enter키로 도달하는 최단거리를 구하면 된다.
(r, c)에서 상하좌우 방향으로 움직일 때 어떤 키에 도달하는지를 전처리를 해 두면 매번 O(1)에 바로 찾을 수 있는데, 이 문제에서는 별도의 전처리 안하고 매번 O(R)에 구해도 통과했다.
풀이: https://www.acmicpc.net/source/share/78aa97a641464f43a931744f016b0afe
공유 소스 보기
#include using namespace std; bool seen[50][50][10001]; char grid[50][51], text[10001]; int R, C, H, dr[] = {1, 0, -1, 0}, dc[] = {0, 1, 0, -1}; int32_t main() { cin.tie(0)->sync_with_stdio(0); cin >> R >> C; for(int i = 0; i < R; i++) { cin >> grid[i]; }
www.acmicpc.net
BOJ 15689 - Catch The Plane
https://www.acmicpc.net/problem/15689
15689번: Catch the Plane
Your plane to the ICPC Finals departs in a short time, and the only way to get to the airport is by bus. Unfortunately, some of the bus drivers are considering going on strike, so you do not know whether you can get to the airport on time. Your goal is to
www.acmicpc.net
문제 요약: 주어진 버스 차편들을 이용해서 최선의 방법으로 이동했을 때, 시간 내로 0번 노드에서 1번 노드에서 도달할 수 있는 확률을 구하는 문제이다. 각 차편은 시작 노드, 도착 노드, 시작 시간, 도착 시간, 차편이 실제로 출발할 확률로 주어지며, 차편이 실제로 출발하는지 여부는 시작 노드에서 시작 시간에 탑승을 시도해야 알 수 있다.
풀이:
"dp[i][t] = i번 노드에 시간이 t초가 되기 전에 이미 도착해 있는 상태일 때, 목적지까지 도달 가능한 확률" 로 정의하자. 처음에는 "dp[1][K+1] = 1"만 확실하고, 나머지 값들을 채워넣어야 한다.
차편이 a, b, s, t, p형식으로 주어질 때, 이 차편 탑승을 시도하거나, 시도하지 않거나 두 가지 경우가 있다. 탑승을 시도하지 않는다면, dp[a][s] 는 단순히 dp[a][s+1]가 된다. 차편 탑승을 시도했을 때는 차편이 출발하거나 출발하지 않거나 두 경우가 있는데, 그래서 dp[a][s] = p * dp[b][t+1] + (1-p)*dp[a][s+1] 꼴로 업데이트를 할 수 있다. 따라서, 각 차편마다 두 가지 경우 중 확률이 더 높은 것을 선택할 수 있다. (같은 시간에 출발하는 차편이 여러 개라면, 그 여러 개의 차편 중에서도 경합해야 한다.)
마지막으로, dp정의를 2차원으로 하면 시간 초과가 난다. 따라서 시간 차원을 떼고, K초부터 0초까지 차편을 도착시간의 역순으로 순회하면서, 각 차편별로 dp[a][s]에 대한 업데이트를 s초에 도달했을 때 미뤄서 수행하는 방식으로 구현하면, 1차원 dp테이블로 같은 알고리즘을 구현할 수 있다.
코드: http://boj.kr/6ba3c4bd0da14ff49f38ad5e536bb370
공유 소스 보기
#include #define int long long using namespace std; struct move_p { int a; double p, prev_dp; }; struct edge { int a, b, s, t; double p; void read() { cin >> a >> b >> s >> t >> p; } }; map , greater > moves; double dp[1000000]; void apply_moves_after(int
www.acmicpc.net
BOJ 23189 - Opportunity Cost
문제: (x, y, z)점 N개가 주어질 때, 아래 식(Opportunity Cost)을 최소화하는 점을 찾는 문제.
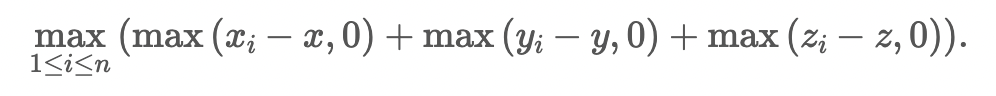
풀이:
점 (x, y, z)를 고정한 상태에서, max(x_i - x, 0) + max(y_i - y, 0) + max(z_i - z, 0)의 최대값을 바로 구하는 방법을 생각해보자. 각 i에 대해서, 총 아래와 같이 2*2*2 = 8가지 경우가 있을 것이다.
- max(x_i - x, 0) 가 zero이거나, nonzero이거나
- max(y_i - y, 0) 가 zero이거나, nonzero이거나
- max(z_i - z, 0) 가 zero이거나, nonzero이거나
이 8가지 경우를 모두 나눠서 생각하면, 식에서 max를 제거할 수가 있어서 최대값 구하기가 매우 간단해진다. 예를 들어서, max(x_i - x, 0)와 max(z_i - z, 0)가 nonzero이고, max(y_i - y, 0)가 zero인 경우에는, 원래 식은 단순히 x_i + z_i - (x + z)가 된다. 즉, max(x_i + z_i)를 미리 전처리해두면 O(1)에 풀 수 있다.
이 때 i번째 점이 8가지 경우 중 어떤 경우에 해당하는지 미리 따질 필요는 없이, max(x_i + z_i)를 모든 점에 대해 전처리해두면 된다. 왜냐하면 i번째 점의 실제 opportunity cost는 i번째 점이 8가지 경우 중 해당하는 경우의 식에서는 정확히 계산되고, 나머지 경우에서는 항상 그보다 높지 않게 계산되기 때문이다.(nonzero인 차원이 식에서 빠지는 것, zero인 차원이 식에 들어오는 것 모두 계산되는 값을 낮춤) 따라서 8가지 경우에 대해서 위와 같이 간소화된 식으로 opportunity cost를 모두 구해 최대값을 취하면, 이 값이 곧 실제 opportunity cost가 된다.
이 방식으로 (전처리 후) 각 점의 opportunity cost를 O(1)에 모두 구하고, 모든 점의 opportunity cost에 대해 최소값을 찾으면 된다.
참고: https://www.youtube.com/watch?v=GwvWvebfL4I&ab_channel=ICPCNews
- Total
- Today
- Yesterday
- dp
- merge sort tree
- subsequence
- offline query
- tree
- induction
- subarray
- segtree
- fenwick
- range query
- 트라이
- 문자열 알고리즘
- bitmask
- 비둘기집의 원리
- 기하
- Counting
- 규칙찾기
- line sweeping
- sqrt decomposition
- GREEDY
- offline
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
